Rachunek prawdopodobieństwa

Definicja prawdopodobieństwa zdarzenia

Prawdopodobieństwo zdarzenia – p jest to stosunek zdarzenia sprzyjającego – n do wszystkich możliwych zdarzeń – N

\sf p =  \cfrac{n}{N}

Jeśli:

• rzucamy raz monetą – N = 2
• rzucamy dwa razy monetą – N = \( 2^2 \) = 4
• rzucamy raz kostką sześcienna – N = 6
• rzucamy dwa razy kostką sześcienną – N = \( 6^2 \) = 36
• rzucamy trzy razy kostką sześcienną – N = \( 6^3 \) = 216

Zauważ, że liczba wszystkich możliwych zdarzeń – N przy rzucie monetą lub sześcienną kostką jest równa liczbie ścian podniesionej do potęgi odpowiadającej liczbie rzutów.

Przykład:

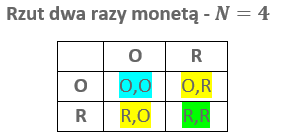
Prawdopodobieństwo wyrzucenie dwóch orłów    \sf \quad p= \cfrac{1}{4}

Prawdopodobieństwo wyrzucenie dwóch reszek   \sf \quad p= \cfrac{1}{4}

Prawdopodobieństwo wyrzucenie reszki i orła (nie ma znaczenie kolejność)       \sf \quad p= \cfrac{2}{4} = \cfrac{1}{2}

Rzut dwa razy sześcienną kostką do gry – N = 36

Tabela w której możemy odczytać jakie liczby możemy wylosować

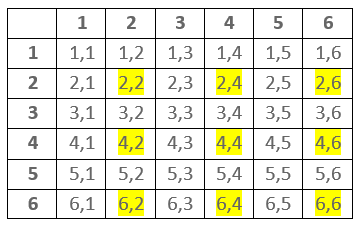
Np. oblicz prawdopodobieństwo wyrzucenia dwóch liczb parzystych       \sf \quad p= \cfrac{9}{36} = \cfrac{1}{4}

Tabela w której możemy odczytać sumę wyrzuconych liczb

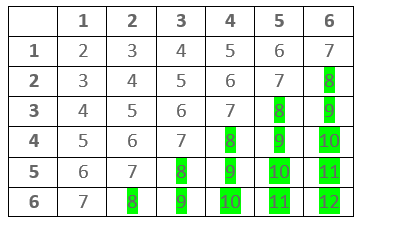
Np. oblicz prawdopodobieństwo wyrzucenie dwóch liczb których suma jest większa od 7

  \sf p= \cfrac{15}{36} = \cfrac{5}{12}

Tabela w której możemy odczytać iloczyn wyrzuconych liczb

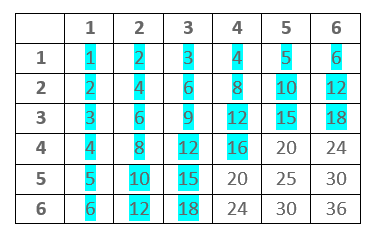
Np. oblicz prawdopodobieństwo wyrzucenie dwóch liczb których iloczyn jest mniejszy od 20

    \sf p= \cfrac{28}{36} = \cfrac{7}{9}  \\[2.5em]

    \\[1em]