Funkcja kwadratowa

Definicja funkcji kwadratowej

Funkcja kwadratowa opisana jest wzorem f(x) = ax² + bx +c, gdzie a ∈ R\{0}, b, c ∈ R.

Dziedziną funkcji jest zbiór liczb rzeczywistych.

Postać ogólna y =ax² + bx +c, gdzie a ∈ R\{0}, b, c ∈ R.

Liczba miejsc zerowych funkcji kwadratowej zależy od wyróżnika (delta)

Δ = b² – 4ac

Postać iloczynowa – postać funkcji wyrażona za pomocą miejsc zerowych

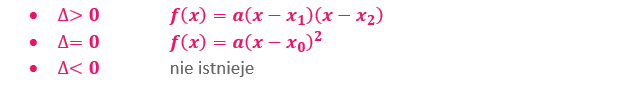
Ramiona funkcji kwadratowej skierowane są:

• do góry, gdy a > 0
• do dołu, gdy a < 0

Postać kanoniczna – postać funkcji wyrażona za pomocą współrzędnych wierzchołka

W = (p,q)

Funkcja kwadratowa i jej własności w zależności od Δ, a

Wzory Viete’a – są to wzory które pozwalają połączyć rozwiązania (pierwiastki) równania kwadratowego z jego współczynnikami, bez konieczności rozwiązywania równania.