Geometria płaska – okrąg i koło

Pole koła i wycinka koła. Długość okręgu i łuku.

Okręgiem o środku O i promieniu r, nazywamy zbiór wszystkich punktów płaszczyzny, których odległość od punktu O jest równa r. Taki okrąg oznaczamy symbolem o(O,r)

Promieniem okręgu nazywamy odcinek łączący środek okręgu z dowolnym punktem tego okręgu.

Cięciwą okręgu nazywamy odcinek łączący dwa dowolne punkty okręgu.

Średnica okręgu to cięciwa przechodząca przez środek okręgu. Średnica jest dwa razy dłuższa od promienia.

Jeśli promień okręgu przechodzi przez środek cięciwy, to jest prostopadły do tej cięciwy.

Jeśli promień okręgu jest prostopadły do cięciwy, to dzieli tę cięciwę na połowy.

Wzajemne położenie prostej i okręgu

Twierdzenie o odcinkach stycznych

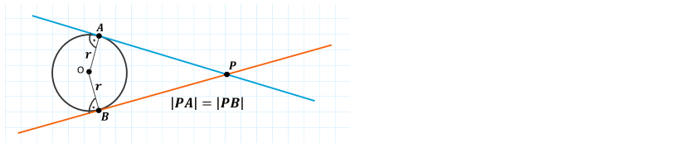
Odcinki dwóch stycznych, poprowadzonych do okręgu z punktu znajdującego się poza okręgiem (czyli w odległości większej niż promień), mają taką samą długość.

Odcinki te są wyznaczone przez punkt zewnętrzny oraz punkty styczności obu stycznych z okręgiem.

Wzajemne położenie dwóch okręgów

Okręgi rozłączne zewnętrznie

Okręgi styczne zewnętrznie

Okręgi przecinające się

Okręgi styczne wewnętrznie

Okręgi rozłączne wewnętrznie

Okręgi współśrodkowe

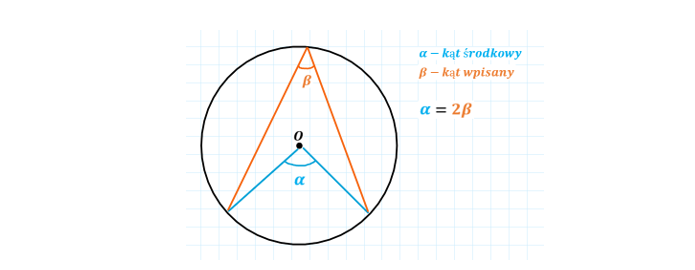
Kąt środkowy to kąt, którego wierzchołek znajduje się w środku okręgu, a jego ramiona są promieniami.

Kąt wpisany to kąt, którego wierzchołek leży na okręgu, a jego ramiona są cięciwami, czyli odcinkami łączącymi punkty na okręgu.

Twierdzenie o stycznej i siecznej

Jeśli dwie proste przecinają okrąg odpowiednio w punktach A i B oraz C i D, a także przecinają się w punkcie P, który znajduje się na zewnątrz okręgu (odległość od środka danego okręgu jest większa niż promień), to iloczyn długości odcinków jednej siecznej (wyznaczonych od punktu przecięcia do punktów przecięcia z okręgiem) jest równy iloczynowi długości odcinków drugiej siecznej.

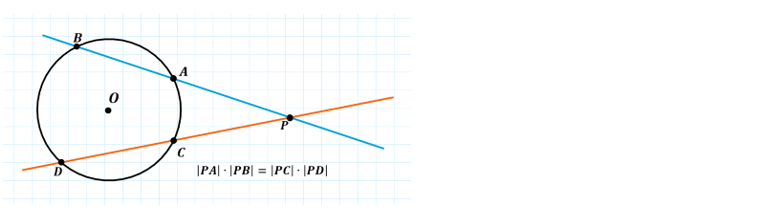
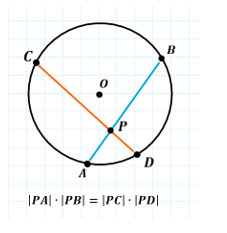
Twierdzenie o cięciwach

Jeśli cięciwy AB  i CD danego okręgu przecinają się w punkcie P wewnątrz okręgu, to |PA|⋅|PB| = |PB|⋅|PD|

Okrąg opisany na trójkącie – symetralna boków trójkąta

Symetralna boku to prosta prostopadła do danego boku trójkąta, która przechodzi przez jego środek. Symetralne wszystkich trzech boków trójkąta przecinają się w jednym punkcie — jest to środek okręgu opisanego na trójkącie.

Trójkąt równoramienny

Trójkąt równoboczny

Trójkąt prostokątny

Środek okręgu opisanego na trójkącie, może znajdować się:

• wewnątrz trójkąta – okrąg opisany na trójkącie ostrokątnym
• na boku trójkąta – okrąg opisany na trójkącie prostokątnym
• poza trójkątem – okrąg opisany na trójkącie rozwartokątnym

Okrąg wpisany w trójkącie – dwusieczna kątów trójkąta

Dwusieczna kąta trójkąta to półprosta wychodząca z wierzchołka kąta, która dzieli ten kąt na dwie równe części.

Dwusieczne wszystkich trzech kątów trójkąta przecinają się w jednym punkcie, który jest środkiem okręgu wpisanego w trójkąt.

Trójkąty równoramienny

Trójkąty równoboczny

Trójkąty prostokątny

Twierdzenie o dwusiecznej kąta w trójkącie

Dwusieczną kąta w trójkącie dzieli przeciwległy bok na odcinki proporcjonalne do pozostałych boków trójkąta