Wektory
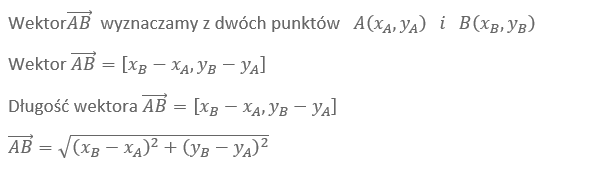
Działanie na wektorach
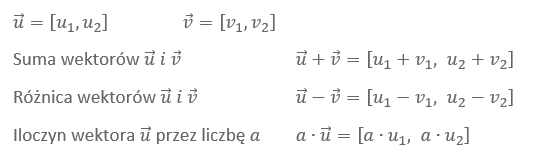
Równanie kierunkowe proste
y = ax + b \quad a = tg α
a – współczynnik kierunkowy
α – kąt nachylenia prostej do osi OX
b – wyraz wolny, miejsce przecięcia osi OY
Wyznaczenie równania prostej przechodzącej przez dwa punkty
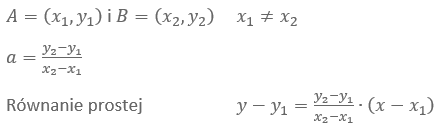
Położenie względem dwóch prostych w postaci kierunkowej, mając
y=a_1x+b_1 \quad y=a_2x+b_2- proste równoległe, gdy \qquad a_1=a_2
- proste prostopadłe, gdy \qquad a_1\cdot a_2 = -1
Równanie ogólne prostej \quad Ax + By + C = 0 \space gdzie \space A^2+B^2 \neq 0
\\ y = -\frac{A}{B}x -\frac{C}{B} \qquad B \neq 0Położenie dwóch prostych w postaci ogólnej, mając
A_1x+B_1y+C_1=0 \qquad A_2x+B_2y+C_2=0- proste równoległe, gdy \qquad A_1B_2-A_2B_1=0
- proste prostopadłe, gdy \qquad A_1A_2+B_1B_2=0
Odległość punktu od prostej
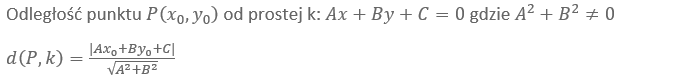
Odległość między dwiema prostymi równoległymi
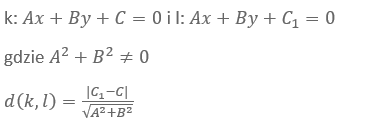
Pole trójkąta ABC o wierzchołkach A=(x_A,y_A), B=(x_B,y_B), C=(x_C,y_C)
Środek ciężkości w trójkącie S=(x_S,y_S)
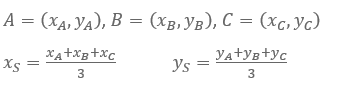
Równanie okręgu. Wzajemne położenie prostej i okręgu
\\ \text{Okrąg wyznacza środek } S=(x_S,y_S) \text{ i promień r}Postać kanoniczna okręgu
\\ (x-x_S)^2 + (y-y_S)^2 = r^2Postać ogólna okręgu
\\ x^2+y^2-2 \cdot x_S \cdot x - 2 \cdot y_S \cdot y + c= 0 \\[-0.5em]
\\ \text{gdzie } c=x^2_S+y^2_S-r^2 \\[-0.5em]
\\ r^2=x^2_S+y^2_S-r^2 -c \\[1.5em]
Położenie prostej k względem okręgu o środku O
- \text{prosta k styczna do okręgu }\qquad d(O,k)=r
- \text{prosta k sieczna okręgu }\qquad d(O,k)<r
- \text{prosta k rozłączna z okręgiem }\qquad d(O,k)>r
Wzajemne położenie dwóch okręgów o_1(S_1,r_1) \, o_2(S_2,r_2)
- \text{są rozłączne zewnętrznie }\qquad |S_1S_2|>r_1+r_2
- \text{są styczne zewnętrznie }\qquad |S_1S_2|=r_1+r_2
- \text{przecinają się }\qquad |r_1-r_2|<|S_1S_2|<r_1+r_2
- \text{są styczne wewnętrznie }\qquad |S_1S_2|=|r_1-r_2|\neq0
- \text{są rozłączne wewnętrznie }\qquad |S_1S_2|<|r_1-r_2|
Sprawdź pozostałe lekcje dla
III klasy liceum
